Der Matrizentest
Du bereitest dich auf einen Einstellungstest vor und fragst dich, was der Matrizentest ist? Die Aufgaben mit den verschiedenen Formen bereiten dir Kopfschmerzen? Wir erklären dir im Folgenden alles Wichtige über diese Testart und wie du die Aufgaben am besten lösen kannst.
Begriffserklärung
Was bedeutet Matrizen? Matrizen ist die Mehrzahl von Matrix. Eine Matrix ist eine tabellarische Anordnung von Daten, die in einer bestimmten Beziehung oder einem Zusammenhang zueinander stehen. Da der vollständige Test jedoch nicht aus einer Matrixaufgabe allein, sondern aus mehreren besteht, entstand der Name Matrizentest.
Geschichtlicher Hintergrund
Woher kommt der Matrizentest? Im Jahr 1938 wurde der erste Test dieser Art veröffentlicht. Der Erfinder heißt John C. Raven. Daher wirst du eventuell auch auf den Namen Ravens Matrizentest stoßen. Der Ravens Matrizentest ist der älteste und bekannteste seiner Art. Er wird am häufigsten als Vorlage für Einstellungstests genutzt.
Neben dem Ravens Matrizentest gibt es noch den Bochumer Matrizentest, den Wiener Matrizentest und eher unbekannte Formen, wie den Formanns averbalen Matrizentest. Alle diese Arten beruhen stets auf dem Ravens Matrizentest. Lediglich der Schwierigkeitsgrad, der Umfang und die genaue Darstellung der Aufgaben können variieren.
Je nach Matrizentest gibt es weitere Unterarten, die für gewisse Altersgruppen angefertigt wurden. Beispielsweise gibt es den Ravens Matrizentest in drei Unterarten:
- Standardform (Bearbeitung ab zehn Jahren)
- Coloured Progressive Matrice (Bearbeitung für Kinder von fünf bis zehn Jahren)
- Advanced Progressive Matrice (Bearbeitung für Hochbegabte ab 16 Jahren)
Zumeist bestehen die einzelnen Arten aus je 60 Aufgaben. Innerhalb eines Einstellungstests musst du im Durchschnitt höchstens fünf Matrizenaufgaben lösen. Der Matrizentest gilt als sprachfrei, was heißt, dass keine sprachlichen Fähigkeiten benötigt werden.
Matrizentest als Intelligenztest
Ziel des Matrizentests ist es, deine allgemeine kognitive Leistungsfähigkeit zu testen. Ein großer Teil dieser kognitiven Leistungsfähigkeit besteht in der sogenannten „eduktiven” Fähigkeit. Die eduktive Fähigkeit lässt dich Beziehungen erkennen, vorhandene Unordnung sortieren und Sinnhaftigkeit in scheinbar zufälligen Anordnungen erkennen. Es werden also deine Wahrnehmung und dein logisches Denken getestet.
Intelligenztests zielen ebenfalls häufig auf die Bereiche Wahrnehmung und logisches Denken ab. Daher kann auch die Schlussfolgerung gezogen werden, dass mit dem Matrizentest indirekt ein Intelligenztest durchgeführt wird.
Aufbau der Aufgaben
Wie bereits erwähnt, bestehen die Aufgaben immer aus einer Matrix. Das heißt, du siehst eine tabellarische Anordnung von Formen und Strichen. Die Größe kann variieren. Normalerweise bestehen Matrizen immer aus mindestens drei Zeilen und drei Spalten. Für Einstellungstests werden die Matrizen jedoch gerne in einer Zeile abgebildet. Eine der Abbildungen wird leer gelassen oder mit einem Fragezeichen gekennzeichnet. Du musst aus meistens vier bis sechs Antwortmöglichkeiten die richtige Abbildung auswählen. Die richtige Abbildung findest du, indem du das Muster der vorherigen Abbildungen erkennst und weiterführst. Wie genau das funktioniert, erklären wir dir in den nächsten Absätzen.
Matrizentests können aus Zahlen, Buchstaben und Figuren bestehen. Die Umwandlung in einzeilige Matrizentests wird als Figurenreihe bezeichnet.
Matrizentest aus Figuren
Innerhalb der Figurenmatrizen gibt es drei grundlegende Regeln, mit Hilfe derer die meisten Tests gelöst werden können. Diese sind die Regeln der Überlagerung, der Fortsetzung und der Variation. Diese Regeln können sowohl auf die Items selbst, als auch auf deren Eigenschaften abzielen. Desweiteren musst du herausfinden, in welche Richtung die Regel angewandt wird. Wenn mehrere Items innerhalb eines Felds zu finden sind, können auch verschiedene Regeln auf die jeweiligen Items zutreffen. Auch die Kombination von Regeln ist nicht ausgeschlossen.
Die Regel der Überlagerung
Die Überlagerung kann auch als Addition verstanden werden. Einfach gesagt werden die Figuren aufeinander, übereinander oder untereinander gegliedert. Diese Regel kann sowohl für die Spalten, als auch für die Reihen gelten. Eine vorgeschriebene Richtung gibt es nicht. Das heißt, die Überlagerung kann von rechts nach links, von links nach recht, von oben nach unten und von unten nach oben stattfinden.
Ein Beispiel:
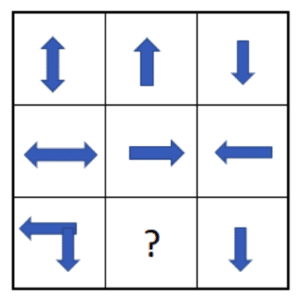
Anhand dieses Beispiels lässt sich die Regel des Überlagerns einfach erklären. Betrachte lediglich die Zeilen von rechts nach links. Dir fällt auf, dass der jeweils erste Pfeil zusammengesetzt mit dem jeweils zweiten Pfeil den dritten Pfeil ergibt. Daher wäre die Lösung dieser Matrix ein Pfeil, der nach links gerichtet ist.
Die Regel der Fortsetzung
Die Fortsetzung ist wohl die einfachste und am schnellsten zu erkennende Regel. Die Spalten oder Zeilen wiederholen sich einfach. Achtung! Hier kann es aber auch sein, dass es nur auf das Muster in den Formen ankommt!
Zwei Beispiele:
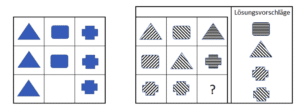
Betrachtest du das erste Beispiel, erkennst du die einfache Fortsetzung der Figuren. Die erste Spalte besteht aus Dreiecken, die zweite Spalte aus Rechtecken und die letzte Spalte aus Kreuzen. Auch wenn du dir die Reihen ansiehst, erkennst du, dass alle Reihen gleich sind. Somit ist die Lösung sehr einfach. Es ist ein Rechteck, das in der dritten Reihe an zweiter Stelle fehlt.
Das zweite Beispiel funktioniert nach dem gleichen Prinzip. Hier musst du jedoch auf das Muster in den Figuren achten. Dadurch erkennst du, dass die dritte Spalte jeweils aus einer Figur mit geradliniger Musterung besteht. Daher ist der oberste Lösungsvorschlag der richtige.
Die Regel der Variation
Die Variation ist sozusagen das Gegenteil der Fortsetzung. Hier wird innerhalb der Spalten oder Reihen abgewechselt. Es gibt keine gleichbleibende Figur oder Musterung in den Reihen.
Zwei Beispiele:
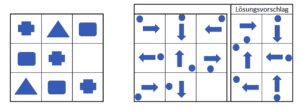
Das erste Beispiel ist auch hier wieder einfach. Sowohl in der Zeile, als auch in den Spalten fällt auf, dass jeweils alle drei Figuren vorhanden sein müssen. Dadurch lässt sich schnell die Lösung „Dreieck” definieren.
Das zweite Beispiel enthält zwei Figuren. Betrachte zuerst die Pfeile. Nach kurzer Analyse fällt auf, dass sich die Pfeile von links nach rechts immer um 90 Grad im Uhrzeigersinn drehen. Wenn du ein gutes Auge hast, fällt dir zudem auf, dass hier die Regel „Fortsetzen” ebenfalls angewandt werden könnte. Die Pfeile der ersten Zeile entsprechen den Pfeilen der dritten Zeile. Das heißt, die Lösung besteht aus einem Pfeil, der nach links zeigen muss. Nun sieh dir die Kreise an. Auch hier fällt auf, dass sie in den Zeilen jeweils im Uhrzeigersinn abwechselnd in einer Eckposition oder mittig auf der Linie liegen. Daraus kannst du schließen, dass der Kreis für die Lösung in der oberen linken Ecke platziert sein muss. Das heißt, die richtige Lösung ist der Lösungsvorschlag der dritten Reihe links.
Matrizentest aus Zahlen
Diese Art des Matrizentests ist ähnlich einer Zahlenreihe. Du musst die mathematische Beziehung der Zahlen herausfinden. Mögliche Beziehungen bestehen in der Addition, Subtraktion, Multiplikation und Division der Zahlen miteinander oder mit einem bestimmten Wert. Häufig werden in der Abbildung Hilfestellungen in Form von Pfeilen gegeben. Diese Pfeile zeigen dir, in welche Richtung die Beziehungen gelten.
Zwei Beispiele:
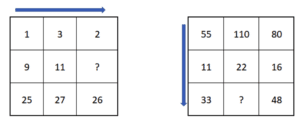
Betrachten wir zuerst das erste Beispiel. Dort wird mit Hilfe eines Pfeils angegeben, dass die Beziehung der Zahlen von links nach rechts in den Zeilen gesucht werden muss. 1 zu 3 könnte durch Addition mit 2 oder Multiplikation mit 3 erreicht werden. Wenn du nun in die zweite Zeile schaust, erkennst du, dass die Multiplikation mit 3 falsch ist, die Addition mit 2 jedoch passt. Gleiches gilt in der dritten Reihe: Von 3 zu 2 und 27 zu 26 funktioniert nur die Subtraktion mit 1. Daher ergibt sich das Beziehungsmuster +2 für die erste und -1 für die zweite Beziehung. Die Lösung ist somit 10.
In zweiten Beispiel besteht eine Beziehung innerhalb der Spalten. 55 zu 11 könnte durch Subtraktion mit 44 oder Division mit 5 erreicht werden. Um dich für die richtige Beziehung zu entscheiden, musst du auch hier wieder in die nächsten Spalten sehen. Dir wird dadurch auffallen, dass es sich um die Division mit 5 handelt. Wenn du in der nächsten Zeile das gleiche Schema anwendest, wirst du die Lösung 66 durch Multiplikation mit 3 finden.
Matrizentest aus Buchstaben
Für diese Art des Matrizentests musst du dir das Alphabet als Referenz vorstellen. Die Matrizen sind nicht mit Zahlen oder Figuren, sondern mit Buchstaben gefüllt. Gleich der Zahlenmatrizen wird ein Pfeil für die Beziehungen vorgegeben.
Ein Beispiel:
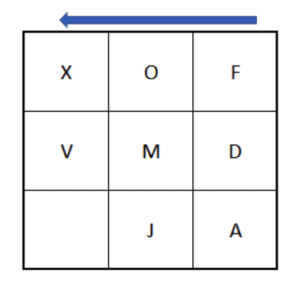
Zuerst musst du dir den Pfeil ansehen. Mit Hilfe des Pfeils erkennst du, dass sich die Beziehungen innerhalb der Zeilen von rechts nach links befinden. Nun musst du in Gedanken das Alphabet durchgehen. Du wirst feststellen, dass von F zu O und von O zu X acht Buchstaben ausgelassen wurden. Dasselbe gilt für D zu M und von M zu V. Um die Lösung zu finden, musst du lediglich im Alphabet ab J acht Buchstaben auslassen. Dadurch erhältst du die Antwort S.
Figurenreihen
Figurenreihen werden gerne als Abwandlung zu Matrizenaufgaben in Einstellungstests genutzt. Der Aufbau und die Lösungswege bleiben gleich, die Figuren befinden sich lediglich in einer Reihe und nicht in einer Matrix. Die Regeln gelten auch hier, sind jedoch oft schwieriger zu erkennen. Achte speziell auf die einzelnen Bestandteile!
Ein Beispiel:
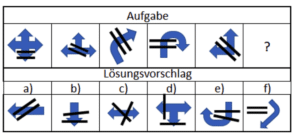
Diese Figurenreihe besteht aus Pfeilen. Auf den ersten Blick trifft keine der obigen Regeln zu. Um auf die richtige Lösung zu kommen, musst du jedes Item betrachten. Für die Pfeile kann keine Beziehung erkannt werden. Alle Pfeile sind blau und zeigen ohne erkennbare Regel in unterschiedliche Richtungen. Die schwarzen Striche liegen jedoch immer auf den Pfeilen und parallel zueinander. Mit dieser Erkenntnis kann die Lösung gefunden werden. Die Striche müssen auf den Pfeilen liegen und parallel zueinander sein. Dadurch ist Lösungsvorschlag a) korrekt.
Vorbereitung auf den Matrizentest
Wir haben dir in den vorherigen Absätzen die wichtigsten Vorgehensweisen erklärt, um Matrizentests zu lösen. Um dich noch besser vorzubereiten, solltest du einige Übungsaufgaben bearbeiten. Diese findest du zahlreich im Internet auf verschiedensten Seiten. Falls du lieber mit Stift und Papier arbeitest, kannst du auch in einem Buchhandel nach Fachbüchern zu Matrizentests fragen.
Fazit
Matrizentests können unterschiedlichster Art sein. Es erfordert je nach Schwierigkeitsgrad ein hohes Maß an Konzentration, um die richtige Lösung zu finden. Mit Hilfe dieses Textes und genug Übungszeit solltest du dich jedoch ohne Probleme auf die Matrizentests für Einstellungstests vorbereiten können.
Das könnte dich noch interessieren
Allgemeinwissen Einstellungstest
Duales Studium Einstellungstest
