Geometrie im Einstellungstest
Ein spezieller Bereich der Mathematik ist die Geometrie. Fragen über Geometrie gehören nicht zu den Standardfragen in Einstellungstests. Für einige Berufe ist die Geometrie jedoch von großer Bedeutung. Wir erläutern dir in diesem Artikel in welchen Berufen gerne Fragen aus der Geometrie genutzt werden und wie diese gestaltet sind. Außerdem geben wir dir Tipps, wie du dich am besten vorbereiten kannst.
Sinn der Fragen
Geometrie ist ein Teilbereich der Mathematik. Mathematische Fragestellungen dienen zur Prüfung, ob du:
- Zusammenhänge erkennst,
- Informationen kombinieren kannst
- und Schlussfolgerungen ziehen kannst.
Geometrie ist da etwas anders. Die Geometrie beschäftigt sich mit dem Raum und der Beschaffenheit von Figuren. Diese können dabei in einer Ebene oder als Körper auftreten. Typische Figuren auf einer Ebene sind zum Beispiel Dreiecke oder Quadrate, während Körper beispielsweise Kugeln oder Quader sind.
Berufe, für die Geometrie von großer Bedeutung sind, sind zum Beispiel:
- Geo- und Umweltinformatiker
- Geomatiker
- Maschinenbautechniker
- Bauzeichner
- Technischer Zeichner
- Fachkraft für Straßen- und Verkehrstechnik
Natürlich gibt es auch entsprechende Studiengänge wie etwa:
- Geometrie und Topologie
- Mathematik
- Technomathematik
Wenn du dich für einen der obigen Berufe oder Studiengänge beworben hast, wirst du sehr wahrscheinlich im Einstellungstest Fragen zur Geometrie finden. Dabei ist der Schwierigkeitsgrad der Fragen natürlich abhängig vom Beruf. Im Einstellungstest zur Ausbildung als Bauzeichner wirst du auf weniger schwierige Aufgaben stoßen wie im Test für den Studiengang Geometrie und Topologie.
Im Folgenden geben wir dir einen Überblick über immer wieder auftretende Fragen aller Berufsrichtungen.
Aufgaben aus der Geometrie
In der Geometrie erwarten dich viele verschiedene Aufgaben. Dazu gehören beispielsweise die Nachfolgenden:
- Winkelberechnung
- Koordinatensystem
- Umfangberechnung
- Flächeninhalte
In Einstellungstests werden Aufgaben zu Flächeninhalten und zum Umfang am häufigsten gestellt. Dabei werden normalerweise Figuren aus der Ebene genutzt. Am gängigsten sind Quadrate, Rechtecke, Parallelogramme, Dreiecke, Kreise und Trapeze.
Du kannst den Umfang aller Figuren errechnen, indem du alle Seitenlängen addierst. Für den Flächeninhalt benötigst du zum Teil kleine Formeln.
Wir geben dir im Folgenden Beispiele zu allen gängigen Figuren.
Quadrat
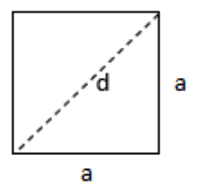
Ein Quadrat zeichnet sich dadurch aus, dass alle Seitenlängen (a) gleich lang sind. Das Quadrat besitzt vier 90°-Winkel.
Du kannst den Umfang (U) somit ganz einfach mit 4 x a berechnen. Damit du den Flächeninhalt (A) berechnen kannst, musst du die Formel A = a x a oder A = a² nutzen.
Beispiel:
- Das Quadrat hat eine Seitenlänge von fünf Zentimetern.
- U = 4 x 5cm = 20cm
- A = 5cm x 5cm oder (5cm)² = 25cm²
Rechteck
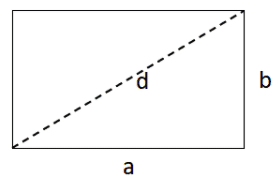
Bei einem Rechteck sind jeweils die gegenüberliegenden Seiten gleich lang und parallel zueinander. Auch ein Rechteck hat vier 90°-Winkel.
Den Umfang (U) kannst du mit 2 x b + 2 x a berechnen. Diese Formel kannst du zu 2 x (a + b) vereinfachen. Für den Flächeninhalt (A) multiplizierst du die Seitenlänge a mit der Seitenlänge b.
Beispiel:
- Das Rechteck hat die Seitenlängen sechs Zentimeter (a) und vier Zentimeter (b).
- U = 2 x (6cm + 4cm) = 20cm
- A = 6cm x 4cm = 24cm²
Parallelogramm
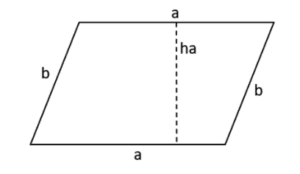
Die gegenüberliegenden Seitenlängen eines Parallelogramms verlaufen ebenfalls parallel. Der Unterschied zwischen einem Parallelogramm und einem Rechteck liegt in den Winkeln. Ein Parallelogramm besitzt keinen 90°-Winkel. Die Gradzahl der Winkel ist variabel, jedoch sind immer die gegenüberliegenden gleich.
Wie du dir vermutlich bereits gedacht hast, kannst du den Umfang (U) mit der gleichen Formel, wie die des Rechtecks, berechnen. Für den Flächeninhalt (A) musst du die Seitenlänge (a) mit der Höhe (ha) multiplizieren.
Beispiel:
- Ein Rechteck hat die Seitenlängen acht Zentimeter (a) und sechs Zentimeter (b). Die Höhe entspricht sieben Zentimeter (ha).
- U = 2 x (8cm + 6cm) = 28cm
- A = 8cm x 7cm = 56cm²
Trapez
Trapeze gibt es in verschiedenen Varianten:
- Gleichschenklige Trapeze
- Rechtwinklige Trapeze
- Gewöhnliche Trapeze
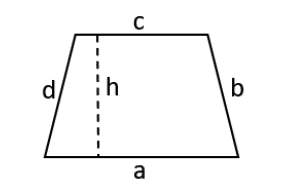
Generell sind Trapeze immer so aufgebaut, dass zwei Seiten (a und c) parallel zueinander sind. Die Länge dieser beiden Seiten ist jedoch nie gleich. Die anderen beiden Seiten (b und d) verbinden dann die Enden der Parallelen. Bei einem gleichschenkligen Trapez sind die beiden Schenkel (b und d) gleich lang. Ein rechtwinkliges Trapez zeichnet sich durch einen rechten Winkel zwischen einem Schenkel zu den Parallelen aus.
Es spielt für die Berechnung des Umfangs (U) und des Flächeninhalts (A) keine Rolle, welche Art von Trapez dir vorliegt. Du kannst den Umfang immer als Summe aller Seitenlängen berechnen (a + b + c + d). Den Flächeninhalt erhältst du, indem du folgende Formel mit der zusätzlichen Angabe der Höhe (h) nutzt: A = (a + c) / 2 x h.
Beispiel:
- Dir ist ein Trapez mit den folgenden Daten gegeben:
Seitenlängen: zwölf Zentimeter (a), vier Zentimeter (b), neun Zentimeter (c) und fünf Zentimeter
Höhe (h): drei Zentimeter- U = 12cm + 4cm + 9cm + 5cm = 30cm
- A = (12cm + 9cm) / 2 * 3cm = 31,5cm²
Dreieck
Auch Dreiecke lassen sich in drei Gruppen unterteilen:
- Rechtwinkliges Dreieck
- Gleichschenkliges Dreieck
- Gleichseitiges Dreieck
Rechtwinkliges Dreieck
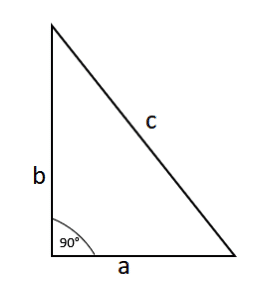
Rechtwinklige Dreiecke zeichnen sich dadurch aus, dass es einen rechten Winkel im Dreieck gibt.
Du kannst den Umfang (U) berechnen, indem du alle Seiten summierst. Um den Flächeninhalt (A) zu erhalten, verwendest du die folgende Formel: A = a x b / 2
Beispiel:
- Das rechtwinklige Dreieck hat die nachstehenden Seitenlängen: a = vier Zentimeter, b = 8 Zentimeter und c = zehn Zentimeter.
- U = 4cm + 8cm + 10cm = 12cm
- A = 4cm x 8cm / 2 = 16cm²
Gleichschenkliges Dreieck
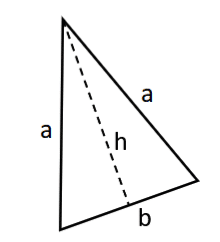
Bei einem gleichschenkligen Dreieck sind zwei Seitenlängen gleich lang. Die Winkel können verschieden sein.
Der Umfang (U) lässt sich bei einem gleichschenkligen Dreieck sehr einfach mit 2 x a + b berechnen. Der Flächeninhalt (A) ist etwas komplizierter. Du hast die Möglichkeit mit der Höhe (h) zu rechnen. Ist die Höhe gegeben, lautet die Formel A = 0,5 x b x h. Hast du die Höhe jedoch nicht gegeben, kannst du auch mit den Seitenlängen den Flächeninhalt berechnen. Dafür nutzt du diese Formel: 0,5 x b x Wurzel aus (a² – b² / 4).
Beispiel:
- Du hast ein gleichschenkliges Dreieck mit den folgenden Seitenlängen gegeben: zweimal neun Zentimeter (a) und sechs Zentimeter (b). Die Höhe (h) beträgt achteinhalb Zentimeter.
- U = 2 x 9cm + 6cm = 24cm
- A = 0,5 x 6cm x Wurzel aus [(9cm)² – (6cm)² / 4] = 25,5cm²
oder
- A = 0,5 x 6cm x 8,5cm = 25,5cm²
Gleichseitiges Dreieck
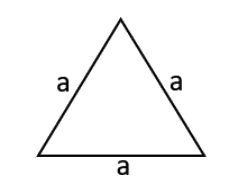
Ein gleichseitiges Dreieck hat sowohl drei gleich lange Seitenlängen als auch gleiche Winkel (immer 60°).
Um den Umfang (U) zu berechnen, kannst du somit einfach 3 x a rechnen. Die Formel für den Flächeninhalt (A) ist etwas komplizierter: A = a² / 4 x Wurzel aus 3.
Beispiel:
- Dir ist ein gleichseitiges Dreieck mit einer Seitenlänge von 8 Zentimeter vorgegeben.
- U = 3 x 8cm = 24cm
- A = (8cm)² / 4 * Wurzel aus 3 = 27,7cm²
Kreis
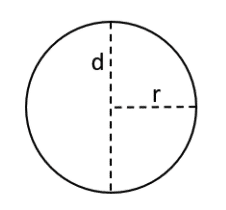
Für Aufgaben mit einem Kreis hast du immer entweder den Radius (r) oder den Durchmesser (d) gegeben. Der Radius ist dabei immer die Hälfte des Durchmessers. Für die Berechnung des Umfangs und des Flächeninhalts wird die Konstante „Pi” benötigt. Pi hat immer einen Wert von gerundet 3,14.
Damit du den Umfang (U) berechnen kannst, musst entweder Pi x 2 x r oder Pi x d rechnen. Für den Flächeninhalt (A) wird die Formel Pi x r² genutzt.
Beispiel:
- Der gegebene Kreis hat einen Radius von fünf Zentimetern.
- U = Pi x 2 x 5cm = 31,4cm
oder
U = Pi x 10cm = 31,4cm
- A = Pi x (5cm)² = 78,5cm
Tipps zur Vorbereitung
Damit du dich optimal auf die Fragen zur Geometrie vorbereiten kannst, solltest du einige Übungsaufgaben absolvieren. Du findest verschiedene Aufgaben mit unterschiedlichen Schwierigkeitsgraden entweder im Internet oder in deinen Schulsachen.
Präge dir die Formeln gut ein. Solltest du keinen Taschenrechner verwenden dürfen, wirst du ziemlich sicher keinen Kreis berechnen und keine Wurzeln ziehen müssen.
Je nachdem, für welchen Beruf du dich beworben hast, kann es auch sein, dass dir andere Daten gegeben werden. Beispielsweise wird dir für eine beliebige Figur bereits der Flächeninhalt gegeben. Deine Aufgabe besteht dann darin, eine Seitenlänge zu berechnen. Wenn du die Formeln beherrschst, kannst du diese ganz leicht umstellen.
Eine gute Möglichkeit, dir die Formeln besser merken zu können, sind Erklärvideos, wie die Formeln entstehen. In diesen Erklärvideos wird dir Schritt für Schritt gezeigt, wie die Formeln entstehen. Dadurch kannst du dir die Formeln viel einfacher einprägen, da es kein reines Auswendiglernen mehr ist. Solltest du während des Einstellungstests eine Formel vergessen haben, kannst du sie dir dann ganz einfach selbst ableiten. Schreibe dir am besten während der Prüfung die Formeln an den Rand des Arbeitsblattes oder auf einen Notizzettel. So vergisst du sie nicht.
Fazit
Geometrische Aufgaben werden in Einstellungstests nicht regelmäßig gestellt. In einigen Berufen spielt die Geometrie jedoch eine große Rolle. Wenn Fragen über Geometrie gestellt werden, handelt es sich häufig um Flächen- und Umfangberechnungen. Am häufigsten werden Quadrate, Rechtecke, Parallelogramme, Trapeze, Dreiecke und Kreise genutzt. Der Umfang lässt sich meistens einfacher berechnen als der Flächeninhalt. Du solltest dich mithilfe deiner Schulhefte auf die Aufgaben vorbereiten. Mit einer guten Vorbereitung wirst du die Fragen problemlos lösen können.
Das könnte dich noch interessieren
Geometrie im Einstellungstest – Dreiecke, Kreise, Quadrate,… ?
Kreatives Denken im Einstellungstest mit Bravour meistern – Informiere dich hier!
Biologie im Einstellungstest – Was ist ein Gen?
Politik im Einstellungstest – Am Jurawissen soll’s nicht scheitern! Inklusive Beispielfragen!
Erdkunde im Einstellungstest – Was sind Polarlichter? Ist Russland Teil Asiens?
