Zinsrechnung im Einstellungstest
Dir steht ein Einstellungstest bevor und das Thema Zinsrechnung bereitet dir ein wenig Sorgen? Erst einmal herzlichen Glückwunsch! Denn die erste Hürde des Bewerbungsverfahrens hast du erfolgreich gemeistert und du wurdest zum Einstellungstest eingeladen. Im nachfolgenden Artikel schauen wir uns die Zinsrechnung ein wenig genauer an und bieten dir ebenfalls einige Beispielaufgaben hierzu.
Zinsrechnung im Einstellungstest
Immer mehr Arbeitgeber setzen beim Einstellungstest nicht nur auf ein rein mündliches Vorstellungsgespräch, um sich ein Bild von dir zu machen. Oftmals besteht der Einstellungstest aus einem schriftlichen Teil, in welchem du neben berufsbezogenen Fragen auch in vielen unterschiedlichen Themengebieten getestet wirst. Darüber hinaus können auch mündliche Testverfahren oder ein Assessment-Center während des Einstellungstests auf dich zukommen. Auf diese Weise können Arbeitgeber deine Fähigkeiten beurteilen und feststellen, ob die ausgeschriebene Stelle zu dir passt.
Mathematik ist hierbei bei so gut wie jedem Beruf ein Teil des schriftlichen Einstellungstests. Ob du im Verwaltungswesen, als Feuerwehrmann, Polizist oder in kaufmännischen Berufen arbeitest, spielt hierbei meist keine große Rolle. Mathematik, insbesondere die Grundrechenarten, sollte jeder Mensch beherrschen, weshalb du hiermit in jedem Einstellungstest rechnen solltest. Lediglich der Schwierigkeitsgrad der Mathematikaufgaben unterscheidet sich je nach Art des Berufs.
Zinsrechnung ist ein Bereich der Grundrechenarten und wird in den Einstellungstests meist mit anderen Aufgaben vermischt. Hierbei kann es sein, dass dir Fragen im Multiple-Choice-Stil gestellt werden und du als Antwort auf eine Textaufgabe die korrekte Antwort auswählen musst. Im nachfolgenden beschäftigen wir uns etwas genauer mit der Zinsrechnung.
Bist du fit für deinen Einstellungstest? Finde es heraus!
Zinsrechnung – was ist das eigentlich?
Genaugenommen ist die Zinsrechnung eine Anwendung des Prozentrechnens. Fällt es dir schwer, die Zinsrechnung im Allgemeinen nachzuvollziehen? Schau dir auch das Prozentrechnen noch einmal etwas genauer an, hierzu kann dir unser Artikel Einstellungstest Prozentrechnung helfen. Während Einstellungstests werden häufig Aufgaben der Prozent- und der Zinsrechnung miteinander vermischt, weshalb du beides beherrschen solltest.
Der Name Zins stammt ursprünglich aus dem Lateinischen und bedeutet so viel wie Vermögensschätzung. Bei der Zinsrechnung werden Geldbeträge berechnet, die ein Gläubiger für das zur Verfügung stellen von Geld an einen Schuldner verlangt. Die sogenannten Zinsen zahlst du also für die Leistung, Geld von einer anderen Person in Anspruch genommen oder ausgeliehen zu haben.
Beispielsweise möchtest du dir ein Auto kaufen, hast jedoch nicht ausreichend Geld zur Verfügung und leihst dir mithilfe eines Kredits Geld bei einer Bank. Damit die Bank dir für einen festgelegten Zeitraum Geld zur Verfügung stellt, zahlst du ihr als Schuldner Zinsen. Aber auch andersrum ist es möglich: Legst du dein Geld auf einem Sparbuch an, darf die Bank mit deinem Geld arbeiten und zahlt dir dafür eine Gegenleistung. Auch diese Gegenleistung wird als Zinsen betitelt und erhöht am Ende das Guthaben auf deinem Sparbuch.
Ein Schuldner ist immer derjenige, der Geld leiht und somit die Zinsen schuldet und ein Gläubiger derjenige, der das Kapital zur Verfügung stellt.
Die Höhe der Zinsen ist nicht immer gleich, da diese sich nach der Betragshöhe, dem Zeitraum und dem vereinbarten Zinssatz richtet.
Zinsrechnung und Prozentrechnung – der Unterschied
Wie bereits gesagt, sind die Prozent- und die Zinsrechnung sehr eng miteinander verknüpft und das Rechnen gestaltet sich ziemlich gleich. Während es sich beim Prozentrechnen aber um verschiedene Einheiten, Werte und Größen handelt, geht es bei der Zinsrechnung immer um Geld. Bei der Zinsrechnung werden etwas andere Begrifflichkeiten verwendet, welche aus der Finanzwirtschaft kommen:
- Kapital: Beim Kapital handelt es sich bei der Zinsrechnung in der Regel immer um das Start- oder Anfangskapital vor der Verzinsung. Bei der Prozentrechnung würde man hierbei vom Grundwert sprechen.
- Zinsen: Das Geld, welches du für das Leihen von Kapital von einer anderen Person zahlst. Bei der Prozentrechnung würde man in diesem Fall vom Prozentwert sprechen.
- Zinssatz: Mithilfe des Zinssatzes berechnest du die zu zahlenden oder zu erhaltenden Zinsen. Bei der Prozentrechnung würde man hier vom Prozentsatz sprechen. In der Regel wird ein Zinssatz immer für ein ganzes Jahr angegeben, weshalb er oftmals mit dem Kürzel „p.a.” angegeben wird. Die Abkürzung „p.a.” kommt aus dem Lateinischen „per anno” und heißt übersetzt „pro Jahr”.
Zinsrechnung: Die verschiedenen Formeln
Damit du während deines Zinsrechnung-Einstellungstests die Aufgaben verstehst, schauen wir uns nun einmal die Formeln und Abkürzungen der Zinsrechnung genauer an. Beginnen wir mit der Zuordnung der Abkürzungen, welche wir dir in der nachfolgenden Tabelle verdeutlicht haben:
Das Prozentzeichen ist hier eingeklammert, da es in den Formeln der Zinsrechnung entfällt und lediglich das „p” bestehen bleibt. Beim Anwenden der Zinsformel setzt du somit nur den entsprechenden Wert ohne Angabe des Prozentzeichens ein.
Die Berechnung von Zinsen für einen Zeitraum von einem Jahr
Beginnen wir mit der Berechnung von Zinsen für einen Zeitraum von einem Jahr. Wir legen einen bestimmten Geldbetrag für einen Zeitraum von einem Jahr an und wollen ausrechnen, wie hoch die Zinsen sind, die wir hierfür erhalten.
Um die Höhe der Zinsen als Betrag auszurechnen, multiplizieren wir unser Startkapital mit dem entsprechenden Zinssatz. Addierst du diesen Zinsbetrag mit unserem Startkapital, erhältst du das neue Kapital, auch Endkapital genannt, welches wir nach Gutschrift der Zinsen erhalten.
Wandeln wir das Ganze in Formeln um, sieht es so aus:
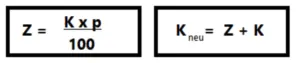
Z = Zinsen
K = Startkapital
p = Zinssatz
K neu = Endkapital
Beispielaufgabe:
Herr Müller legt ein Kapital von 4.000 Euro ein Jahr lang zu einem Zinssatz von 2,6% an. Wie hoch ist das Endkapital von Herrn Müller nach diesem Jahr?
Setzt du nun die Angaben in die Zinsformel ein, berechnest du die zu erhaltenen Zinsen:
Z = (K x p) : 100
Z = (4.000€ x 2,6) : 100 = 104€
Die Aufgabenstellung lautete jedoch, das Endkapital von Herrn Müller zu errechnen.
Aus diesem Grund musst du die 104€ Zinsen zum Startkapital von 4.000€ hinzuaddieren:
K neu = Z + K
K neu = 104€ + 4.000€ = 4.104€
Die Lösung dieser Aufgabe lautet somit:
Herr Müller erhält ein Endkapital von 4.104 Euro.
Was tun, wenn andere Werte gefragt sind?
Bei der Zinsberechnung kann es sein, dass du anstelle der Zinsen eventuell den Zinssatz oder das Kapital berechnen sollst. In diesem Fall musst du die Zinsformel einfach umstellen:
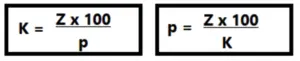
K = Startkapital
Z = Zinsen
p = Zinssatz
Beispielaufgabe 1:
Nehmen wir wieder das Beispiel von Herrn Müller:
Herr Müller erhält 104€ Zinsen zu einem Zinssatz von 2,6%. Wie hoch war das Startkapital von Herrn Müller?
K = (Z x 100) : p
K = (104€ x 100) : 2,6 = 4.000€
Lösung:
Das Startkapital von Herrn Müller betrug 4.000 Euro.
Beispielaufgabe 2:
Herr Müller legt ein Kapital von 4.000€ für einen Zeitraum von einem Jahr an und erhält 104€ Zinsen. Zu welchem Zinssatz hat er das Kapital angelegt?
p = (Z x 100) : K
p = (104€ x 100) : 4.000€ = 2,6%
Lösung:
Der Zinssatz betrug 2,6 Prozent.
Die Berechnung von Zinsen für einen Zeitraum von einem Monat
Nicht alle Kredite oder Geldanlagen haben einen Zeitraum von einem oder mehreren vollen Jahren. Es ist ebenso möglich, Geld für einen oder mehrere Monate anzulegen oder zu leihen. Um die Zinsen korrekt auszurechnen, musst du in diesem Fall die Anzahl der Monate in die Zinsformel integrieren.
Das Kapital wird hier mit dem Zinssatz sowie der Anzahl der Monate multipliziert. Im Anschluss teilst du den ermittelten Wert durch 100 x 12, da ein Jahr aus zwölf Monaten besteht. Du ergänzt also die Zinsformel um die Monate – und zwar über dem Bruchstrich. Unterhalb des Bruchstriches ergänzt du die Zahl zwölf, welche für ein vollständiges Jahr steht. Möchtest du wieder unterschiedliche Werte ermitteln, kannst du die Formel entsprechend umstellen:
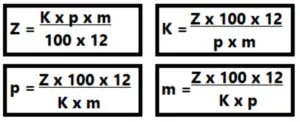
Z = Zinsen
K = Startkapital
p = Zinssatz
m = Monate
Beispielaufgabe 1:
Herr Müller legt sein Eigenkapital von 4.000€ für einen Zeitraum von acht Monaten, zu einem Zinssatz von 2,6% an. Wie viele Zinsen erhält Herr Müller für die acht Monate?
Z = (K x p x m) : (100 x 12)
Z = (4.000€ x 2,6 x 8) : (100 x 12) = 69,33€
Lösung:
Herr Müller erhält für die Anlage von acht Monaten 69,33€ Zinsen.
Beispielaufgabe 2:
Herr Müller erhält 69,33€ Zinsen, wenn er sein Kapital von 4.000€ für einen Zeitraum von acht Monaten anlegt. Zu welchem Zinssatz legt Herr Müller sein Kapital an?
p = (Z x 100 x 12) : (K x m)
p = (69,33€ x 100 x 12) : (4.000€ x 8) = 2,6%
Lösung:
Herr Müller legt sein Kapital zu einem Zinssatz von 2,6% an.
Beispielaufgabe 3:
Herr Müller legt Eigenkapital für einen Zeitraum von acht Monaten zu einem Zinssatz von 2,6% an und erhält 69,33€ Zinsen. Wie viel Eigenkapital hat Herr Müller angelegt?
K = (Z x 100 x 12) : (p x m)
K = (69,33€ x 100 x 12) : (2,6 x 8) = 4.000€
Lösung:
Herr Müller hat ein Eigenkapital von 4.000€ angelegt.
Beispielaufgabe 4:
Herr Müller legt sein Kapital von 4.000€ bei der Bank zu einem Zinssatz von 2,6% an. Am Ende erhält er 69,33€ Zinsen. Für wie lange hat Herr Müller sein Kapital angelegt?
m = (Z x 100 x 12) : (K x p)
m = (69,33€ x 100 x 12) : (4.000€ x 2,6) = 8
Lösung:
Herr Müller hat sein Eigenkapital für acht Monate angelegt.
Die Berechnung von Zinsen für einen Zeitraum von einem Tag
Natürlich ist es auch möglich, Zinsen für einen oder mehrere Tage auszurechnen. In diesem Falle fügst du der Zinsformel nicht die Anzahl der Monate hinzu, sondern der entsprechenden Tage.
Aber Achtung! Anders als bei den normalen Kalenderjahren hat ein Monat bei der kaufmännischen Zinsrechnung immer 30 Tage und somit ein Jahr 360 Tage!
Diese Rechnung verhält sich überall in Deutschland gleich, im Ausland kann es hierzu Abweichungen geben.
Ähnlich wie bei der Berechnung von monatlichen Zinsen erweiterst du die Formel um zwei Angaben. Oberhalb des Bruchstriches vermerkst du die entsprechenden Tage, unterhalb die 360, die für ein Jahr steht.
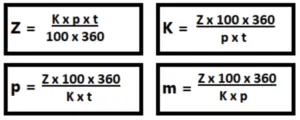
Z = Zinsen
K = Kapital
p = Zinssatz
t = Tage
Beispielaufgabe 1:
Herr Müller legt sein Kapital von 4.000€ mit einem Zinssatz von 2,6% an und zahlt es am 1. März ein. Da Herr Müller sein Geld allerdings schon bald wieder benötigt, hebt er es am 22. April wieder ab. Wie viele Zinsen erhält Herr Müller?
Um die gestellte Aufgabe zu lösen, musst du erst einmal die Tage ausrechnen, für die Herr Müller sein Geld angelegt hat. Da Herr Müller sein Kapital direkt am 1. März eingezahlt hat, ist somit ein vollständiger Monat – sprich 30 Tage – vergangen. Der 22. April, der Tag der Abhebung, wird allerdings nicht mehr berücksichtigt, weshalb du für den April noch 21 Tage hinzurechnen musst. Addierst du die beiden Werte zusammen, kommst du auf 51 Tage, die Herr Müller sein Kapital bei der Bank angelegt hat. Nun kannst du alle Werte in die entsprechende Formel eintragen, um die Zinsen zu berechnen.
Z = (K x p x t) : (100 x 360)
Z = (4.000€ x 2,6 x 51) : (100 x 360) = 14,73€
Lösung:
Herr Müller erhält 14,73€ Zinsen.
Beispielaufgabe 2:
Herr Müller hat sein Eigenkapital für einen Zeitraum von 51 Tagen zu einem Zinssatz von 2,6% angelegt und erhielt 14,73€ Zinsen. Wie hoch war das Eigenkapital von Herrn Müller?
K = (Z x 100 x 360) : (p x t)
K = (14,73€ x 100 x 360) : (2,6 x 51) = 4.000€
Lösung:
Herr Müller hat ein Kapital von 4.000€ angelegt.
Beispielaufgabe 3:
Herr Müller hat ein Kapital von 4.000€ für einen Zeitraum von 51 Tagen angelegt und 14,73€ Zinsen erhalten. Zu welchem Zinssatz hat er sein Kapital bei der Bank angelegt?
p = (Z x 100 x 360) : (K x t)
p = (14,73€ x 100 x 360) : (4.000€ x 51) = 2,6%
Lösung:
Der Zinssatz der Bank betrug 2,6%.
Beispielaufgabe 4:
Herr Müller hat sein Eigenkapital von 4.000€ zu einem Zinssatz von 2,6% angelegt und 14,73€ Zinsen erhalten. Wie lange hatte Herr Müller sein Kapital angelegt?
t = (Z x 100 x 360) : (K x p)
t = (14,73€ x 100 x 360) : (4.000€ x 2,6) = 51
Lösung:
Herr Müller hat sein Kapital für einen Zeitraum von 51 Tagen angelegt.
Vorbereitung ist alles
Informiere dich im Vorfeld, welche Themen du beim Einstellungstest besonders beherrschen solltest. Danach kannst du dich dann explizit auf diese Themen vorbereiten und bist beim Einstellungstest weniger nervös. Wirf auch noch mal einen Blick in deine Schulbücher, um Beispielaufgaben zu lösen und weitere Erklärungen zu finden. Auch auf unserer Website findest du sämtliche Artikel zu Einstellungstests verschiedener Berufe und den möglichen Themen, die während des Einstellungsverfahrens abgefragt werden können. In den meisten findest du hilfreiche Übungsaufgaben, mit denen du dich auf deinen Zinsrechnung-Einstellungstest vorbereiten kannst. Fühlst du dich danach immer noch ein wenig unsicher, hilft dir vielleicht unser Online-Testtrainer, speziell im Bereich Mathematik, um dich vollständig auf deinen Einstellungstest vorzubereiten.
Fazit
Das Thema Zinsrechnung kann auf den ersten Blick ziemlich verwirrend erscheinen. Prägst du dir allerdings die Grundformeln gut ein, kannst du sie jederzeit der Aufgabenstellung entsprechend umstellen. In der Regel enthält jeder Einstellungstest Aufgaben zur Mathematik und somit meist auch zur Zins- oder Prozentrechnung. Verrückt machen solltest du dich trotzdem nicht: Auch wenn du in diesem Bereich ein paar Fehler machst, wird es nicht das komplette Ergebnis deines Einstellungstests auf den Kopf stellen. Die Zinsrechnung bildet meist nur einen kleinen Bruchteil vom gesamten Einstellungstest. Möchtest du nochmal alle Grundrechenarten etwas auffrischen? Schau dir gern auch unseren Artikel Einstellungstest Mathe an, welcher dir einen Überblick über verschiedene Aufgaben gibt, die dich während deines Einstellungstests erwarten können.
Das könnte dich noch interessieren
Wortanalogien im Einstellungstest – Beispiele aus Deutsch und der Mathematik
Prozentrechnung im Einstellungstest – 100% mit Bravour bestehen!
Geometrie im Einstellungstest – Dreiecke, Kreise, Quadrate,… ?
Allgemeinwissen im Einstellungstest bestehen – Das erwartet dich
Mathematik Einstellungstest einfach bestehen – Der Überblick
