Ableitungsregeln online
Das Konzept der Ableitung ist ein grundlegendes Element der Differentialrechnung und spielt eine entscheidende Rolle in vielen Bereichen der Mathematik, Physik und anderen naturwissenschaftlichen Disziplinen – und wird genau deshalb gerne in Einstellungstests und Prüfungen getestet. In diesem Artikel bekommst du erklärt, wie du einfach mathematische Ableitungen durchführen kannst und findest alle wichtigen Ableitungsregeln online zum nachlesen.
Grundlagen verstehen
Bevor wir uns in die Details der Berechnungen stürzen, ist es wichtig, das Konzept der Ableitung zu verstehen. Die Ableitung einer Funktion f(x) an einem bestimmten Punkt ist definiert als die Rate der Änderung dieser Funktion an diesem Punkt. Mathematisch ausgedrückt ist die Ableitung f'(x) gleich der Grenze des Differenzenquotienten, wenn der Unterschied zwischen zwei Punkten, die sich dem betrachteten Punkt nähern, gegen Null geht.
Die Notation verstehen
Die Ableitung einer Funktion f(x) wird oft mit f'(x) notiert. Diese Notation gibt an, dass es sich um die Ableitung von f in Bezug auf die Variable x handelt.
Ableitungsregeln Übersicht
Es gibt verschiedene Regeln, die wir verwenden können, um Ableitungen zu berechnen. Einige der wichtigsten sind:
Potenzregel
Die Potenzregel besagt, wie man die Ableitung einer Funktion berechnet, die eine Potenz einer Variablen ist. Wenn eine Funktion in der Form f(x) = xⁿ vorliegt , dann ist die Ableitung dieser Funktion f'(x) = nxⁿ ⁻ ¹.
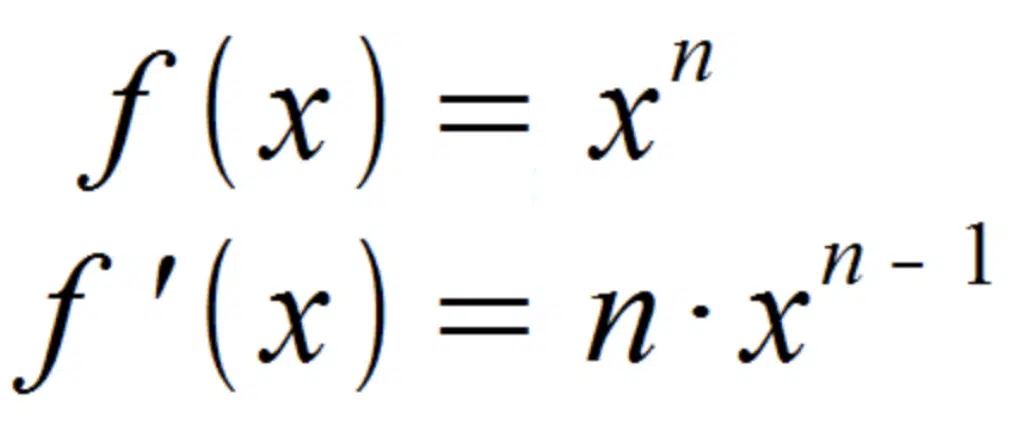
Ein Beispiel: Gegeben ist die Funktion f(x) = x³.
Die Ableitung f'(x) = 3 ⋅ x ³⁻ ¹
f'(x) = 3x².
Summenregel und Differenzregel
Die Summenregel besagt, dass die Ableitung der Summe von zwei Funktionen die Summe ihrer Ableitungen ist. Das heißt, du berechnest die Ableitung jeder Funktion einzeln und addierst dann die einzelnen Ableitungen miteinander.
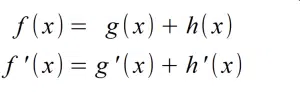
Die Differenzregel funktioniert genauso. Wenn du die Ableitung der Differenz von zwei Funktionen finden möchtest, musst du die einzelnen Ableitungen miteinander subtrahieren.
Wenn f(x) = g(x) – h(x) gilt, f'(x) = g'(x) – h'(x).
Ein Beispiel: Gegeben ist die Gleichung f(x) = 2x + 3x²
2x steht in diesem Beispiel für g(x) und 3x² für h(x). Um die Ableitung f'(x) herauszubekommen, musst du nun die Ableitungen von g(x) und h(x) miteinander addieren. Mathematisch ausgedrückt, sieht das so aus:
f(x) = 2x + 3x²
g(x) = 2x
h(x) = 3x²
Ableitung 1:
g(x) = 2x
g'(x) = 2
Ableitung 2:
h(x) = 3x²
h'(x) = 6x
Ableitung 1 + Ableitung 2:
f'(x) = g'(x) + h'(x)
Antwort:
f'(x) = 6x + 2
Beispiel 2: Gegeben ist die Gleichung f(x) = 2x – 3x²
Die Ableitungen von g(x) und h(x) kennen wir schon aus Beispiel 1.
g(x) = 2x
g'(x) = 2
h(x) = 3x²
h'(x) = 6x
Ableitung 1 – Ableitung 2:
f'(x) = g'(x) – h'(x)
Antwort:
f'(x) = 6x – 2
Die Ableitung der Funktion f(x) = 2x – 3x² ist also f'(x) = 2 – 6x.
Produktregel
Die Produktregel brauchst du immer dann, wenn du eine Funktion, die du ableiten möchtest, ein Produkt aus zwei Teilfunktionen enthält. Optisch erkennst du so einen Fall daran, das zwei mal ein x in der gegebenen Funktionen auf beiden Seiten des Multiplikationszeichens steht.
Die Ableitung des Produkts zweier Funktionen g(x) ⋅ h(x) ist gleich g'(x) ⋅ h(x) + g(x) ⋅ h'(x).
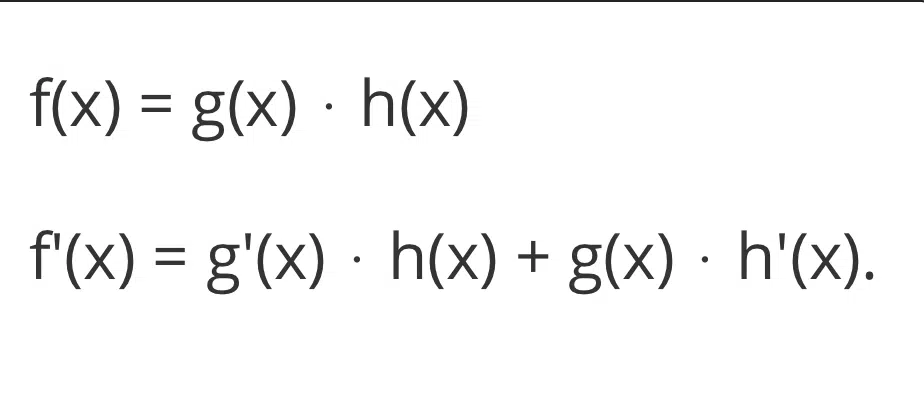
Ein Beispiel: Gegeben ist die Funktion f(x) = x² ⋅ 3x.
Als erstes werden die Ableitungen der einzelnen Funktionen notiert:
g'(x) = 2x h'(x) = 3
Abschließend wird die Ableitung des Produkts gesucht. Dafür verwendest du nun die Produktregel und setzt deine Werte ein. Zur Erinnerung: Die Ableitung nach der Produktregel ist f′(x)⋅g(x) + f(x)⋅g′(x).
Eingesetzt in die Variablen ist das:
f'(x) = 2x ⋅ 3x + x² ⋅ 3
f'(x) = 6x² + 3x²
f'(x) = 9x²
Die Ableitung der Funktion f(x) = x² ⋅ 3x ist also f'(x) = 9x².
Quotientenregel
Die Quotientenregel brauchst du immer dann, wenn du die Ableitung von Funktionen mit Brüchen finden möchtest, also wenn im Zähler und im Nenner des Funktionsbruches ein x vorkommt.
Das heißt, du hast: f(x) = g(x) / h(x)
Um die Funktion f'(x) zu finden gilt:
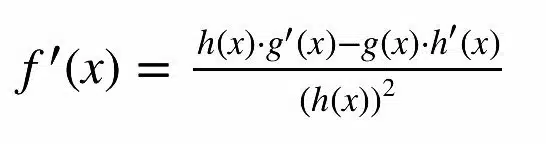
Ein Beispiel: Gegeben ist die Funktion f(x) = (x⁴-3) / x²
In diesem Fall ist
g(x) = x⁴-3 h(x) = x²
g'(x) = 4x³ h'(x) = 2x
Nun wird die Quotientenregel angewandt:
f'(x) = ((x²) ⋅ (4x³)) – ((x⁴-3) ⋅ (2x)) / (x²)²
f'(x) = 4x⁵ – 2x⁵ + 6x / x⁴ Vereinfache nun die Ableitung, indem du 4x⁵ – 2x⁵ rechnest und ein x ausklammerst.
f'(x) = 2x⁵ + 6x / x⁴
f'(x) = x ( 2x⁴ + 6) / x⁴ Kürze nun das ausgeklammerte “x” raus.
f'(x) = 2x⁴ + 6 / x³
Die Ableitung der Funktion f(x) = (x⁴-3) / x² ist also f'(x) = 2x⁴ + 6 / x³.
Kettenregel
Die Kettenregel brauchst du immer dann, wenn eine Funktion g(x) innerhalb einer anderen Funktion f(x) vorkommt, also eine sogenannte verkettete Funktion vorliegt. Eine verkettete Funktion sieht so aus: f(x)= g(h(x))
Um die Funktion f'(x) zu finden gilt:
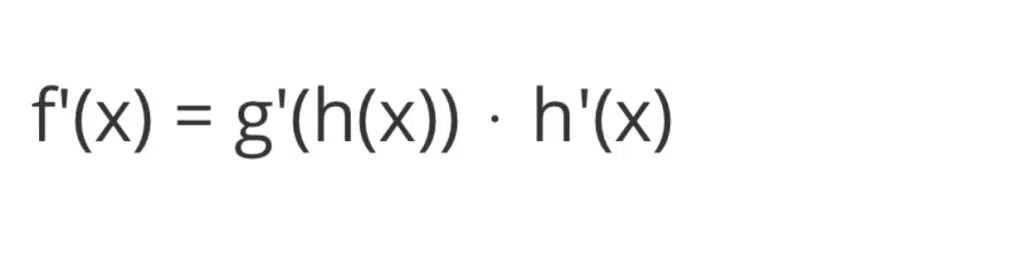
Um die Ableitung von f(x) zu berechnen, wendest du also zuerst die Ableitung auf die äußere Funktion g an, dann multiplizierst du das Ergebnis mit der Ableitung der inneren Funktion h.
Ein Beispiel: Gegeben ist die Funktion f(x) = (x²+4)³
Die äußere Funktion g(x) ist die Potenzfunktion: ()³
Die innere Funktion h(x) ist alles, was in der Klammer steht: x²+4
Nun werden die Ableitungen von g(x) und h(x) bestimmt. Das sind:
g'(x) = 3()²
h'(x) = 2x
Anschließend werden die Werte in die Kettenregel eingesetzt um die Ableitungsfunktion zu bestimmen.
f'(x) = 3(x²+4)² ⋅ 2x
Nun wird noch vereinfacht, indem 3⋅ 2x gerechnet wird:
f'(x) = 6x(x²+4)
Voila! Du hast deine Ableitungsfunktion gefunden. Die Ableitung der Funktion f(x) = (x²+4)³ ist f'(x) = 6x(x²+4).
Ableitungen finden ist gar nicht so schwer
Das war nun vielleicht etwas viel auf einmal. Aber wie bei jedem mathematischen Konzept gilt: Übung macht den Meister! Je mehr Funktionsbeispiele du durchgehst, desto sicherer wirst du werden. Die Ableitungsregeln online sollten dir gut dabei helfen, diese Aufgaben durchführen zu können. Schau auch gern mal in unseren Testtrainer hinein! Hier kannst du zahlreiche Ableitungsaufgaben üben, sodass du richtig fit wirst!
Wir wünschen dir dabei viel Spaß!
